Answer
- Scientific Notation
- E Notation
- Engineering Notation
- Standard Form
- Order of Magnitude
- Real Number
- Word Form
Overview
Scientific notation compresses very large or very small values into one readable coefficient and a power of ten. The key idea: the exponent tracks decimal shifts, while the coefficient carries the meaningful digits.
On this page, you can paste numbers like 33450, 33,450, 3.345e4,
or 3.345 × 10^4, then compare multiple “equivalent” representations side-by-side to catch
exponent mistakes quickly.
What each output means (quick reference)
| Output | Definition | Normalization rule |
|---|---|---|
| Scientific notation | N = a × 10^b |
1 ≤ |a| < 10, b is an integer |
| E notation | aeb (calculator / code friendly) |
Same a and b as scientific |
| Engineering notation | N = a × 10^b |
b is a multiple of 3, 1 ≤ |a| < 1000 |
| Standard form | Full decimal expansion | No exponent; may be long for big/small values |
| Order of magnitude | A scale hint like 10^k |
Often based on k ≈ log10(|N|) |
| Real number | Grouped digits for readability | Uses thousands separators (e.g., 345,600) |
| Word form | English words for the number | Uses short scale (billion = 10^9) |
Common logic mistakes this page helps catch
- Sign errors: confusing
1.2e-4(tiny) with1.2e4(large). - Off-by-one exponent: moving the decimal 5 places but writing
10^-4instead of10^-5. -
Rounding flips: rounding
9.999 × 10^kto10.0 × 10^kwithout renormalizing to1.0 × 10^(k+1).
Formula / Methodology
The normalized scientific form is N = a × 10^b, where b is an integer and
a carries the significant digits. For nonzero N, b is tied to
the base-10 logarithm of the absolute value.
For N ≠ 0: b = floor(log10(|N|)) a = N / 10^b (then adjust if rounding pushes |a| to 10) Engineering form: b_eng = 3 × floor(b / 3) a_eng = N / 10^b_eng with 1 ≤ |a_eng| < 1000
Interpretation tips
- Exponent meaning:
b = 4means “move the decimal 4 places right” to get back to standard form. - Negative exponents:
b = −5means the number is smaller than 1 and has five leading decimal shifts. - Equivalent rewrites: shifting the decimal in
aby one place changesbby one in the opposite direction (value stays identical).
Precision note: for very large magnitudes, browsers may round intermediate values. Use the outputs for comparison and scale checks, not as a substitute for lab-grade precision.
Examples
Example 1: small decimal → scientific / engineering
Input: 0.0000567
- Scientific:
5.67 × 10^-5(decimal moved 5 places right) - E notation:
5.67e-5 - Engineering:
56.7 × 10^-6(exponent multiple of 3) - Order of magnitude (nearest power): near
10^-4
Example 2: large integer with zeros
Input: 98,000,000
- Scientific:
9.8 × 10^7 - Engineering:
98 × 10^6(pairs naturally with “mega”,10^6) - Word form (short scale): “ninety-eight million”
Example 3: equivalent forms (same value, different mantissa)
Input: 3.345e4
- Same value as:
33.45e3and33450 - Scientific:
3.345 × 10^4(preferred normalized form) - Engineering:
33.45 × 10^3(exponent multiple of 3)
Different Number Formats Explained
This tool supports a variety of number input and output formats. Understanding each can help you work efficiently with large or precise values.
Supported Formats
- Scientific Notation: Expresses numbers as a base and power of ten.
Example:3.456 × 10^11 - E Notation: A digital-friendly form of scientific notation.
Example:3.456e11 - Engineering Notation: Similar to scientific, but exponents are multiples of 3 for alignment with SI units.
Example:345.600 × 10^9 - Standard Form: Full decimal form of the number with no exponents.
Example:345600000000.0000000000 - Order of Magnitude: The nearest power of 10 that approximates the number’s scale.
Example:10^11for3.456e11 - Real Number: A readable number with thousand separators for easier comprehension.
Example:345,600,000,000 - Word Form: Converts numbers into English words.
Example:three hundred forty-five billion six hundred million
You can input numbers in any of the following forms:
3.45e7 — E notation3.45 × 10^7 — Scientific notation34,500 — Standard comma-separated number34500000 — Plain numeric inputInfographic & Visual Guide
Two steps do most conversions: (1) place the decimal after the first non-zero digit, (2) count how many places you moved (that count becomes the exponent, with sign).
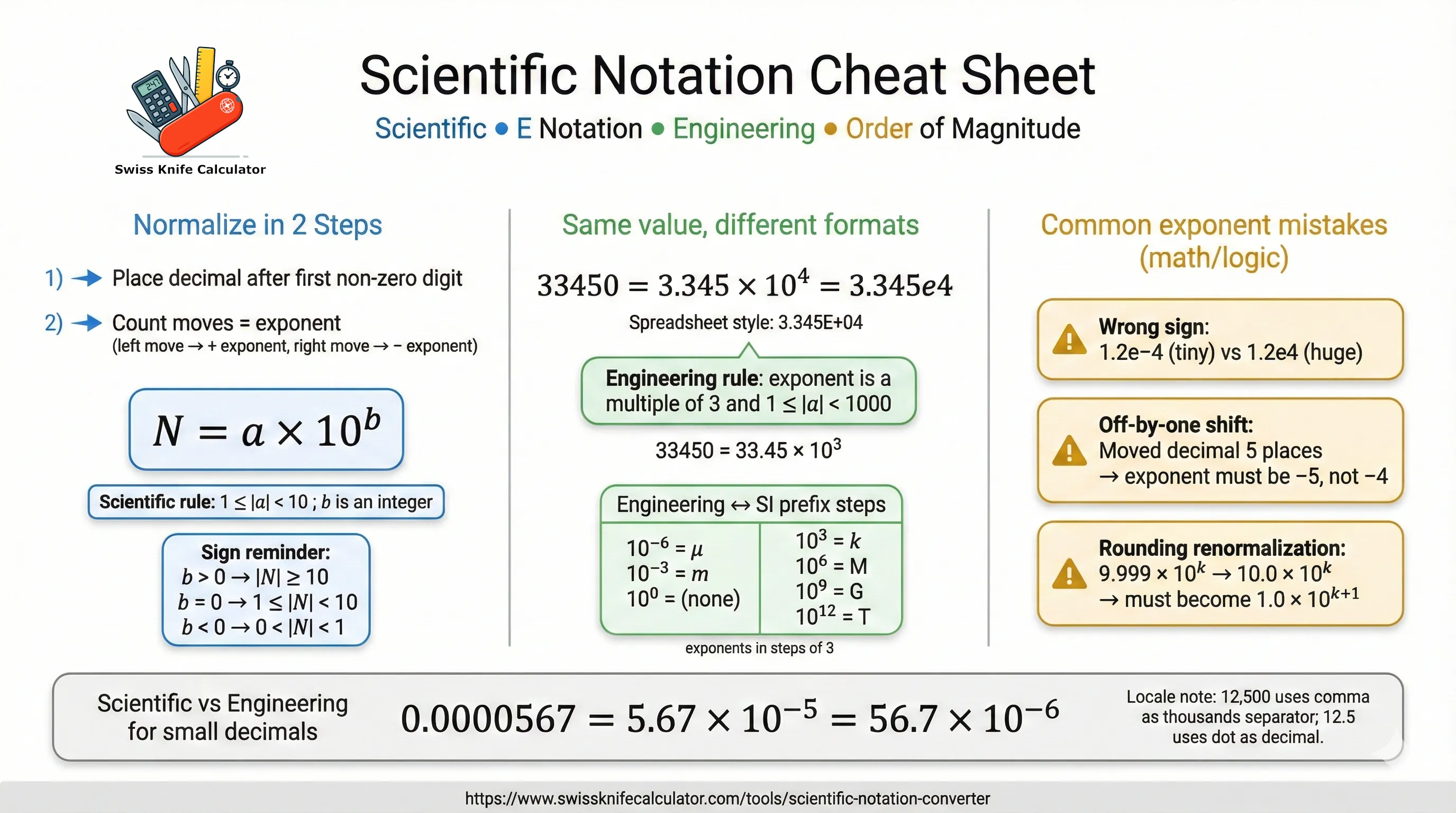
Tip: If you shift the decimal right by 1, the exponent must decrease by 1 (and shifting left increases the exponent). This keeps the value unchanged.
Short scale vs. long scale (word form)
If you grew up with German/French number names, “billion” can be confusing. English word form here follows the short scale.
Large numbers can be described using two main naming conventions: the short scale (used in the US and modern international English) and the long scale (used in many parts of Europe).
Examples of Naming Differences:
| Value | Short Scale (e.g., US) | Long Scale (e.g., Germany, France) |
|---|---|---|
| 10⁶ | Million | Million |
| 10⁹ | Billion | Milliarde |
| 10¹² | Trillion | Billion |
| 10¹⁵ | Quadrillion | Billiarde |
| 10¹⁸ | Quintillion | Trillion |
| 10²¹ | Sextillion | Trilliarde |
| 10²⁴ | Septillion | Quadrillion |
In the short scale, each new term is 1,000 times the previous one (every three zeros). In the long scale, terms alternate between million-based and billion-based naming every six zeros.
Metric Prefixes for Large Numbers (SI Units)
These are used in science and engineering to represent very large quantities:
- Kilo (10³): Thousand
- Mega (10⁶): Million
- Giga (10⁹): Billion
- Tera (10¹²): Trillion
- Peta (10¹⁵): Quadrillion
- Exa (10¹⁸): Quintillion
- Zetta (10²¹): Sextillion
- Yotta (10²⁴): Septillion
- Ronna (10²⁷): Octillion
- Quetta (10³⁰): Nonillion
Understanding these systems is crucial when working with scientific data, computer storage units, and financial or astronomical calculations.
Use Cases
- 🔬 Lab reports & homework: check that your exponent sign matches “bigger than 1” vs “smaller than 1.”
- ⚙️ Engineering calculations: rewrite into exponent steps of 3 to align with SI prefixes (k, M, G, µ, n).
- 📊 Data work: sanity-check CSV / spreadsheet values that appear as
1.23E+07or4.5E-09. - 📈 Finance and analytics: quickly compare scales (millions vs billions) before interpreting charts or forecasts.
Related hubs (internal)
- Unit Converters for other format and unit conversions.
- Data & Computing for math and data utilities.
- Finance when large-number scale matters (millions/billions).
- Time & Date for timestamp and duration helpers that often use scientific notation.
Assumptions & limits
- Locale: expects decimal dot (
12.5) and optional thousands commas (12,500). - Precision: extremely large/small magnitudes may be rounded by browser numeric precision.
- Word form: English short scale naming is used for large numbers.
Educational disclaimer:
This converter is for learning, checking notation, and general calculation support. Results may be approximate
for extreme magnitudes due to rounding and formatting conventions.
Reference: Engineering notation aligns with SI prefix steps (powers of 10 in multiples of 3) as commonly summarized in the BIPM SI Brochure.
Last review: January 2026
FAQ
What input formats can I paste into the converter?
You can paste plain numbers, comma-grouped numbers (e.g., 33,450), decimals, E notation (e.g., 3.345e4), or ×10^ style (e.g., 3.345 × 10^4).
Why must the scientific-notation coefficient be between 1 and 10?
In normalized scientific notation N = a × 10^b, the coefficient a is chosen so that 1 ≤ |a| < 10. This makes the exponent b a clean count of decimal shifts and keeps a unique standard form.
How is engineering notation different from scientific notation?
Engineering notation uses an exponent that is a multiple of 3, so it lines up with SI prefixes (k, M, G, µ, n). The coefficient is then in the range 1 ≤ |a| < 1000 instead of 1 ≤ |a| < 10.
What does “order of magnitude” mean on this page?
Order of magnitude is a power of ten that summarizes scale. A common convention is 10^k where k ≈ log10(|N|) (often rounded to the nearest integer for a quick scale comparison).
Are 3.345e4 and 33.45e3 the same number?
Yes. Shifting the decimal in the coefficient and compensating in the exponent keeps the value identical: 3.345 × 10^4 = 33.45 × 10^3 = 33450.
How are negative numbers handled?
The sign stays on the coefficient. For example, −33450 becomes −3.345 × 10^4 (and −3.345e4 in E notation).
What happens if the input is 0?
Zero has no meaningful exponent in logarithms, so converters use a practical convention. You should see 0 in standard/real/word form, and a scientific-style display like 0 × 10^0 may be used for consistency.
Can rounding change the exponent?
Yes. If rounding makes the coefficient hit 10 (e.g., 9.999 rounds to 10.0), the notation must renormalize to 1.0 × 10^(b+1). This is a common source of off-by-one exponent surprises.
Why does the word form use “billion” for 10^9?
English word form typically uses the short scale, where 10^9 is “billion” and 10^12 is “trillion.” Some European languages use a long-scale naming (e.g., German “Milliarde” for 10^9).
How should I interpret commas and decimal separators?
This page expects a dot for decimals (12.5) and commas as thousands separators (12,500). If your locale uses decimal commas, rewrite 12,5 as 12.5 before converting.
Is there a maximum size this converter can represent?
Browsers use finite-precision numbers for many operations, so extremely large or tiny values may be rounded. For very large exponents, treat results as approximate unless the page explicitly shows full-precision handling.
Where do the SI prefix powers (k, M, G, µ, n) come from?
Engineering notation aligns exponents in steps of 3 to match SI prefixes. The standard prefix powers are defined by the International System of Units (SI) and commonly referenced in the BIPM SI Brochure.
