Enter Value & Units
Result
Converted: –
Scientific: –
Grouped: –
Overview
Angle units look similar on paper, but they measure two different things: rotation in a plane versus spread in 3D space. Mixing those categories is the fastest way to get a “reasonable-looking” number that is completely wrong.
Plane angles describe turning: degrees (°), radians (rad), gradians (gon), arcminutes (′), arcseconds (″), and mils. Solid angles describe how much of the surrounding sphere a shape covers: steradians (sr), square degrees (sq°), and spats.
Where each family shows up
- Math/physics: radians and steradians dominate formulas and models (see Energy tools for more physics-oriented calculators).
- Surveying/GIS: degrees–minutes–seconds (DMS) and gradians are common (browse Home & DIY tools for measurement workflows).
- Astronomy & imaging: arcminutes/arcseconds and square degrees are standard for sky coverage.
- 3D graphics & rendering: solid angle connects directly to light distribution and field coverage (see Data tools for related computation utilities).
Quick reference landmarks (helps catch mistakes)
| Landmark | Degrees | Radians | Gradians (gon) | NATO mil (approx.) |
|---|---|---|---|---|
| Full turn | 360° | 2π | 400 | 6400 |
| Half turn | 180° | π | 200 | 3200 |
| Right angle | 90° | π/2 | 100 | 1600 |
| Small angle | 1° | π/180 ≈ 0.0174533 | 1.111111… | ≈ 17.7778 |
If your conversion makes a right angle come out far from 90°, π/2, or 100 gon, it’s almost always a unit-family mix-up or a wrong mil standard.
More unit tools live in Unit Converters.
Formula/Methodology
Reliable conversion starts by mapping every unit to a single base unit: radians for plane angles and steradians for solid angles. Then convert from the base to the target.
Plane angle base (radian): θ(rad) = θ(from) × k_from θ(to) = θ(rad) ÷ k_to Key plane relationships: rad = deg × (π/180) deg = rad × (180/π) gon = deg × (400/360) = deg × (10/9) deg = gon × (360/400) = gon × (9/10) arcmin = deg × 60 arcsec = deg × 3600
For solid angles, the definition ties directly to area on a sphere: Ω = A / r². On the unit sphere (r = 1), steradians numerically equal the surface area they cut out.
Solid angle base (steradian): Ω(sr) = Ω(from) × k_from Ω(to) = Ω(sr) ÷ k_to Square degrees ↔ steradians: 1 sr = (180/π)² sq° 1 sq° = (π/180)² sr Sphere totals: Full sphere = 4π sr = 1 spat ≈ 12.56637 sr Full sphere ≈ 41252.96125 sq°
Common math/logic mistakes (and how to spot them)
- Forgetting the square in solid angles: converting sq° ↔ sr uses (π/180)², not (π/180). If you’re off by ~57×, you likely missed the square.
- Treating “mil” as universal: “mil” depends on the standard (NATO 6400 per circle is common). If your reference uses a different circle division, results will disagree by a few percent.
- Mixing arcminutes with time minutes: arcminutes are 1/60 of a degree, not “minutes of time.” The symbols look similar in some contexts.
- Assuming wrapping rules are part of the unit: negative angles and angles above 360° can be valid; wrapping (mod 360°) is a convention you apply after converting.
| Unit | What it represents | Anchor fact (quick check) |
|---|---|---|
| Radian (rad) | Arc length equals radius (s = r) | 2π rad per circle |
| Gradian (gon) | Decimal division of a circle | 400 gon per circle; 100 gon per right angle |
| Arcminute (′) | 1/60 of a degree | 60′ per degree |
| Arcsecond (″) | 1/3600 of a degree | 3600″ per degree |
| Steradian (sr) | Area on unit sphere | 4π sr per full sphere |
| Square degree (sq°) | Area measure on the sky | ≈ 41252.96 sq° per full sphere |
Examples
1️⃣ 45° to radians
Use rad = deg × (π/180).
45 × π/180 = π/4 ≈ 0.785398 rad.
2️⃣ 200 gon to degrees
A full circle is 400 gon = 360°, so multiply by 0.9.
200 gon × 0.9 = 180°.
3️⃣ 3° 30′ to degrees (DMS step that’s often missed)
Convert minutes as base-60: 30′ = 30/60° = 0.5°.
So 3° 30′ = 3.5° (then convert to radians if needed).
4️⃣ 7200″ (arcseconds) to degrees
1° = 3600″, so divide by 3600.
7200″ ÷ 3600 = 2°.
5️⃣ 2 sr to square degrees
Use sq° = sr × (180/π)².
2 × (180/π)² ≈ 6565.6127 sq°.
Infographic & Visual Guide
Plane angle is “how far you turned.” Solid angle is “how much of the sphere you cover.” The key mental model: steradians measure area on the unit sphere, so they scale with a squared factor rather than linearly with degrees.
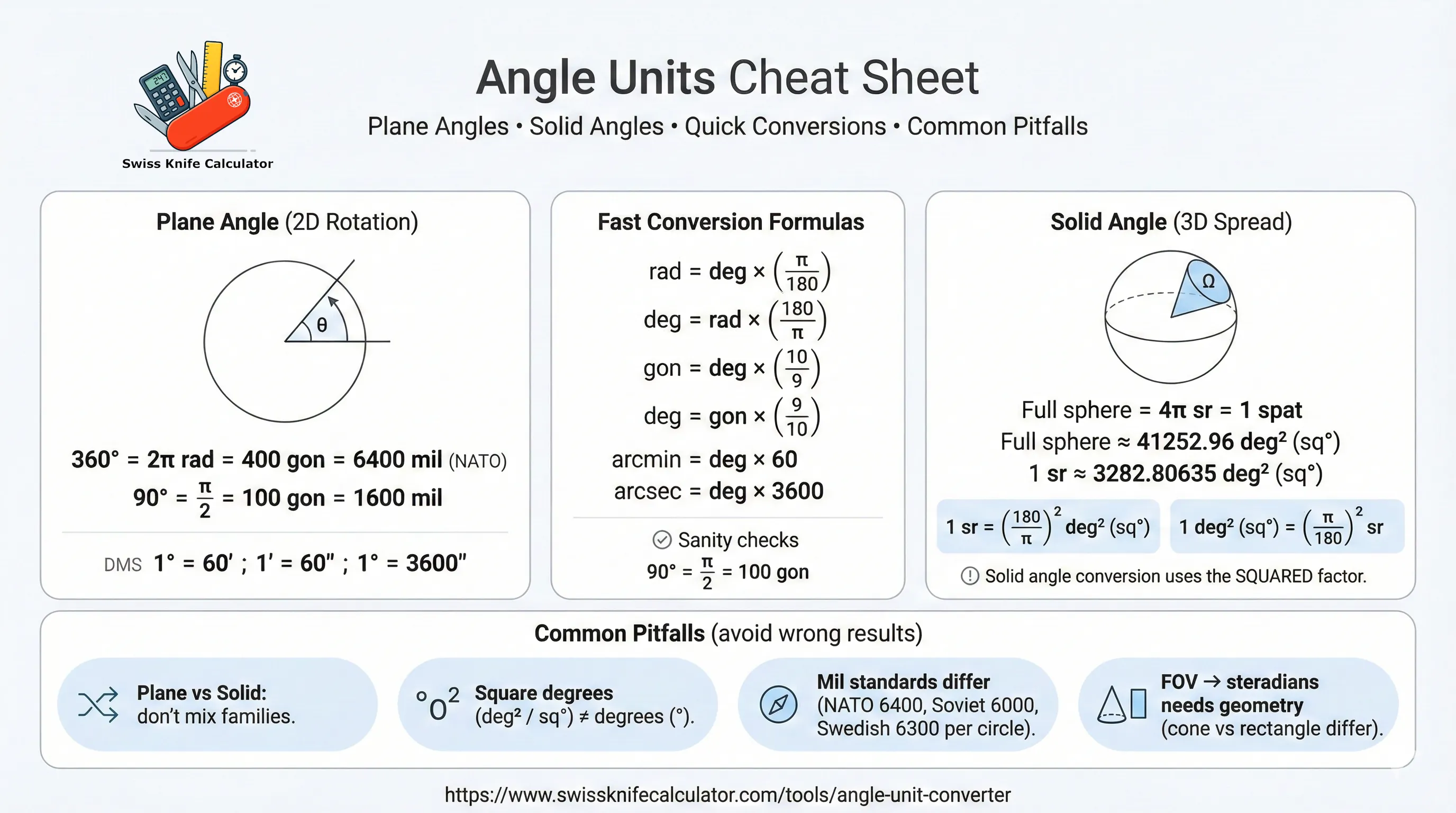
Field-of-view note (important edge case)
If you only know a single “FOV in degrees,” you usually cannot convert it to steradians without geometry. A cone, a rectangle, and an ellipse with the same “angle” can cover different solid angles.
- Circular cone (full angle θ): Ω = 2π(1 − cos(θ/2)).
- Rectangular sensor: you need both horizontal and vertical FOV (or sensor size + focal length) to estimate Ω.
Use Cases
- Surveying & construction layout: gradians (gon) simplify decimal subdivisions; DMS is common for bearings and GIS handoffs.
- Astronomy and imaging: arcminutes and arcseconds describe tiny separations; square degrees describe sky survey coverage.
- Military ranging/aiming: mil values are used in reticles and angular corrections; always confirm which mil definition your reference uses.
- Lighting and radiometry: steradians connect to intensity distribution and coverage in 3D models.
- Math and simulation: radians reduce errors in trig formulas and numerical methods when derivatives are involved.
Typical ranges (useful for sanity checks)
- Plane angles: common wrap is 0–360° (0–2π rad), but negatives and values above one turn can be meaningful.
- Solid angles: physically 0–4π sr for a closed sphere around a point; values above 4π indicate a modeling or unit mistake.
FAQ
What is the difference between a plane angle and a solid angle?
A plane angle measures rotation in 2D (degrees, radians, gradians). A solid angle measures 3D spread around a point (steradians, square degrees, spats).
When should I use radians instead of degrees?
Use radians in trigonometry and calculus formulas, because derivatives and integrals assume radian measure. Use degrees for human-readable bearings, drawings, and many engineering specs.
How do I convert degrees to radians quickly?
Multiply degrees by π/180. For example, 90° equals π/2 rad, and 45° equals π/4 rad.
What is a gradian (gon)?
A gradian (gon) divides a full circle into 400 parts, so a right angle is 100 gon. It is common in surveying because it aligns with base-10 subdivision.
What does “mil” mean, and why can it be ambiguous?
Mil is an angular unit used in ranging and aiming, but different standards exist (for example 6400 mil per circle in NATO). If your source does not specify the standard, confirm it before comparing values.
How many arcminutes and arcseconds are in one degree?
1 degree equals 60 arcminutes, and 1 arcminute equals 60 arcseconds. That means 1 degree equals 3600 arcseconds.
What is a steradian in plain language?
A steradian is the solid angle that cuts out an area of 1 square unit on the surface of a sphere with radius 1. It is the 3D analogue of radians.
How many steradians and square degrees are in a full sphere?
A full sphere is 4π steradians (about 12.56637 sr). In square degrees that is about 41252.96125 sq°.
Can I convert a field-of-view in degrees to steradians directly?
Not from a single degree value alone, because the shape matters (cone, rectangular sensor, circular aperture). For a circular cone with full angle θ, the solid angle is Ω = 2π(1 − cos(θ/2)).
Why do solid-angle conversions square the degree-to-radian factor?
Square degrees measure area on the unit sphere, so the linear conversion must be squared. That is why 1 sq° equals (π/180)² sr, and 1 sr equals (180/π)² sq°.
What is a spat?
A spat is the solid angle of a full sphere. 1 spat equals 4π steradians.
What are typical valid ranges for angles and solid angles?
Plane angles are often wrapped to 0–360° (or 0–2π rad), but negative angles are valid mathematically. Solid angles are physically between 0 and 4π sr for a closed surface around a point.
Disclaimer (educational): Conversions here are mathematical unit conversions and reference values. For critical surveying, ballistic, optical, or calibration work, verify the unit standard (especially mil definitions) and the underlying geometry before relying on results.
Last review: December 2025
